Binary number representations

| Lecture #2: Numbers, numerals and bases |
Binary number representations  | Ones and zeros many different kinds of information can be represented in "binary" form, but the medium of representation is always the same: sequences of bits (ones and zeros) |


| Lecture #2: Numbers, numerals and bases |
Binary number representations  | Ones and zeros |
 | Counting with sequences of bits a sequence of bits of length k can "count" or represent up to 2k different things; i.e., there are 2k different possible combinations of 1s and 0s
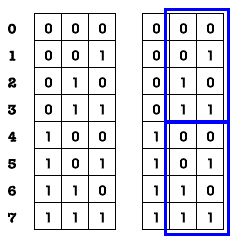 |


| Lecture #2: Numbers, numerals and bases |
Binary number representations  | Ones and zeros |
 | Counting with sequences of bits |
 | Representing choices conversely, we need about log2 (n) bits to represent n different things ("about" here means round up to the nearest whole bit) |


| Lecture #2: Numbers, numerals and bases |
Binary number representations  | Ones and zeros |
 | Counting with sequences of bits |
 | Representing choices |
 | Review laws of logarithms and exponents Here are a few handy laws to remember when working with bases, logs and powers
• • • • • • |
