CS 353 Lab #10: Compiling Simple Expressions

The problem description
Informal semantics
Some sample expressions
Code generation

The problem description

You should write a compiler that reads in an infix expression in the simple language we have been working on for the last couple of labs -- it should produce PC-231 assembly code that will evaluate the expression when run. You should then either use your own assembler and simulator from earlier in the semester or the ones I have provided (or any combination thereof) to convert the assembly code into PC-231 machine language and to run this code.

You should already have a parser and appropriate expression/tree classes available from your work on the last two assignments. Once you have a tree representing a (valid) expression, you can traverse it in right-to-left, bottom-up order to produce assembly code (this is the "back end" of the compiler). (Note that this traversal order is the same as for your interactive evaluator.)

It may be difficult to complete the compiler for the whole language all at once. I recommend taking a progressive approach, so that you implement only a few language features at a time. Adding fancier features in "layers" will allow you to keep a more-or-less complete working program at various checkpoints along the way, so that you have something to turn in should a deadline arrive.

More informal semantics

We took a brief look at informal semantics for each of the different expression forms in lecture and in the notes for the last lab. Here is a more detailed description of each expression form, along with some remarks relevant to code generation (all remarks are made under the assumption that you'll use the PC-231 for your compilation target):

integer literals (sequences of digits only) mean exactly what you would expect, i.e., they are just non-negative, decimal numerals. Recall that the PC-231 has only 11 bits plus a sign bit to work with, and thus can only handle integers whose absolute value is smaller than 2048 (i.e., -2047 to +2047). You might want to generate an error upon seeing a numerals whose value is larger than 2047 (again, you need only handle non-negative literals). Note that literal values will need to be held in a RAM location or (much better!) in some register. Smaller values can be put in a register with a SET command, but larger values will need a DATA command and then a COPY, or a DATA, LOAD and COPY.
Examples: "0", "1", "10", "235", "2047".
variables are essentially storage locations on the PC-231 (either in RAM or in registers) interpreted as holding integer values. This means that they can be set, using assignment, or read, just by mentioning their names as part of an expression. Variable names are lowercase only and may not include digits. You may want to enhance your symbol table from Lab 2 to keep track of where variables are being stored (unless you move them around, e.g. from registers to RAM, in order to free up temporary registers).
Examples: "x", "y", "abc", "xyz".
the READ token is a simple means of allowing our expressions to involve user input. When the READ token is evaluated, the effect should be to read a decimal integer in from the user, using the decimal device ("DD") of the PC-231. The decimal reader provided with the sim231 simulator takes care of all the details of number conversion (including negative numbers), so you need only generate machine code which performs the read itself.
assignment expressions are similar to those used in C, C++ and Java. Their constituents are a variable and an expression: the expression should be evaluated and the value stored in the variable. Note that the value of the assignment expression is the value of its constituent expression, i.e., the same value which is stored in the variable.
Examples: "x=3", "y=y++", "z=READ+x", "2*(n=READ+1)".
the prefix and postfix operators include just the increment (++) and decrement (--) operators familiar from C, C++ and Java. Note that these operators can only be applied to variables, not to arbitrary expressions. Just as in C and Java, when these operators are written postfix, the meaning is that the variable's value is modified after it's value is returned as the result of the expression. In other words, in order to evaluate the expression, we first stash the current value of the variable for the result, then operate on the value of the variable, and then return the stashed value as the result of the expression as a whole. When written in prefix position, these operators update the value of the variable and return the updated value.
Examples: "x++", "x=y++", "x+++y++", "p~~".
the binary operators include the usual multiplication, addition and subtraction operators. Evaluation is done from right to left, i.e., the right argument is evaluated first, then the left. This is important because of the interaction of variables with assignment and the postfix operators: consider the expression "x+x+x=6". According to the precedence and associativity, rules this should clearly be parsed the same as "x+(x+(x=6))", but this does not address the issue of how the expression should be evaluated. Assume for example that the value of x was 4 prior to evaluating this expression: then we might evaluate left-to-right and return results equivalent to "4+4+6" or right-to-left and return results equivalent to "6+6+6". Here we choose right-to-left order.
Since multiplication is not supported directly on the PC-231, you'll need to implement this as in-line code, a sub-routine call or in terms of SHIFT instructions.
Examples: "2+3", "2*(3+x)", "10-x*2+y=3".
The READ expression returns a value read from the user, dynamically. Note that this happens at the time the expression is evaluated, so you must generate code to read in a value from the user (the PC-231 READ expression is the obvious thing to use, in decimal mode, into a register used to temporarily hold the value).
Examples: "READ".
The WRITE expression writes the value of its sub-expression out, but has that same value as its value. This is useful for debugging your expressions, and I usppose for simulating more complex statement-like behavior, but it doesn't have any effect on the expression itself.
Examples: "WRITE 2", "2+(WRITE x=3)".

Some sample expressions

Here is a set of sample expressions you might want to test your compiler on, along with the results they should produce. Note that several of the expressions involve the READ construct, and therefore depend on the values that a user types in at run time.

(2+3)*2
produces: 10 (addition is done first, then multiplication).
2+3*7-1
produces: 22 (multiplication is done first, then subtraction, and finally the addition).
2*x*x + 3*x=7 + 2
produces: 189
READ + READ * 2
produces: 37 (assuming the first (rightmost) READ yields 15 and the second (leftmost) READ yields 7).
x*x+++10-x=3
produces: 19 (note that the expression parses as "((x*(x++))+10)-(x=3)"; the value of the rightmost x is 3, the value of the middle x is also 3, and the value of the final x is 4 because of the ++).
2*x+++10-x=3+x=READ
produces: 18 (assuming the value read is 5; note that the expression parses out as "((2*(x++))+10)-((x=3+(x=READ)))"; the result then follows from right-to-left evaluation. x is left with the value 4).
(Special thanks to Fletcher for spotting a correction or two above!)

Basic plan of action

As described above, your basic approach should be to use your previous labs to read in an expression (as a String), then parse it into a tree form (you may wish to re-print it for debugging purposes), and then traverse the tree to produce PC-231 assembly language. You may also wish to use some form of intermediate code (e.g., for a simple stack machine, as demonstrated in lecture): in this case, you would need to make a final pass over the intermediate code in order to convert it into aaembly code. In either case, in the final phase you would use an assembler (mine or your own) and a simulator to demonstrate that the code actually runs and produces correct results.

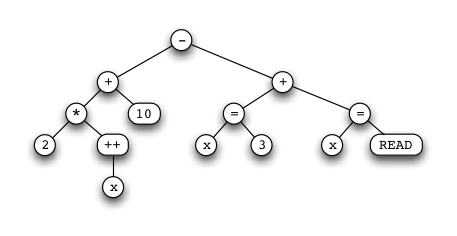
Zac, this is not the tree you are looking for!

(Note that this tree is not the same as the one from the previous lab: it clearly resulted from parsing something more like "2*x+++10-((x=3)+x=READ)".)

Once you have a tree to work with, your code generator can traverse the tree in a right-to-left fashion (to parallel the order of evaluation), producing code as it goes. Along the way, you may need access to some sort of simple symbol table, e.g., to record where variables are stored in memory (alternatively, you could just use labels for the variables in storage and depend on the assembler to do this work for you). One difficult part of code generation concerns the allocation of registers: you may in general build up quite a few temporary results in registers which are "pending", i.e., in use at any given time. One approach to this is to use a "free list" which shows which registers are free. When you compute the result of, say, an addition operation, you will have over-written some register with the result but may be able to re-claim (as "free") the other register operand for use in further evaluation.

The issue of register allocation can be simplified consiuderably by storing temporary results or simulating an operand stack in memory, rather than in registers: using RAM will be considerably slower and may use up so many instructions that you won't be able to compile a larger expression. Use whichever strategy you wish, but be aware of the limitations of your own compiler.

In general, there are a number of places where errors might be caught: do your best to catch any errors you think are reasonable (consult with me if you are unsure), but try to concentrate on handling correct expressions properly. You can always add more error checking (or more sophisticated error reports) at a later time. ‚Pé -->

Code generation

Code generation is largely a process of traversing the parse tree in a bottom-up, right-to-left order, producing code to implement each of the operators, literals or variable references encountered along the way.

You will also need some general strategies for handling registers and RAM locations. In order to generate code for an integer literal, you will need to put it into some register, and you will need to know which ones are free for this purpose. Assuming that register R3, for example, is free, you might generate code like this for the integer literal 5:

	DATA 5
	COPY DR,R3

You will also need to know which register the result of a given sub-tree is stored in, so that the node above it can access it properly. For example, if the integer literal 5 from above occurs as a sub-tree of an addition operator node, you will want to generate code such as the following:

	DATA 5		; from above
	COPY DR,R3	; from above
	
	ADD R2,R3	; assuming other argument was in R2
			; result of the "+" node is in R3
			; and now R2 is free again

As mentioned in above, you can use a free register list in order to keep track of register usage. This list can then be modified as you pass from node to node in the tree. In the example above, you would remove R3 from the list as you passed through the node for the integer literal 5, and then add R2 back into the free list after passing through the addition operator node.

It is possible that a straight-forward use of registers will leave you with no free registers at certain points in the process, especially for larger expressions. If this happens, make sure you are using the free list properly, but you need not go the length of "spilling" registers out into RAM locations. In other words, it is OK if your algorithm fails for some large expressions, as long as you are doing your best to free registers as you go. (Note that if you use RAM for temporary values or the operand stack, you won't need to worry so much about register usage.)

Variables can be handled by setting aside a RAM location for them and then loading them into a register and proceeding as above (i.e., noting the register used in the node somehow). For example, an expression such as "x=(x+2)" might compile as follows:

			; code for int lit "2"
	DATA 2		; int literal 2
	COPY DR,R0	; R0 now in use
	
			; code for var "x"
	DATA #X		; label for var x storage
	LOAD R1,DR	; load x using DR indirectly
	
			; code for op "+"
	ADD R0,R1	; free up R0, result in R1
	
			; code for assignment to "x"
	DATA #X		; set up for store using DR
	STORE R1,DR	; store x, result in R1
	
	. . .		; etc., etc.
			
	HALT		; end of program
	
#X	CONST 0		; placeholder for x
#Y	CONST 0		; placeholder for y
	. . .		; etc., etc.

Handling the multiplication operation will be a bit tougher than the rest: you will need to jump out of the main line of evaluation to a "subroutine" which implements multiplication for you, and then jump back when it is finished. You may use your multiplication routine from a previous lab for this, but note that you will need to do some extra work to make sure that you have left registers for the multiplier to use, a register for the result, and a couple of jump registers for the "call" and "return".

The various other kinds of expressions are much easier to handle. You should probably try generating machine code for some simple expressions by hand until you are comfortable with the techniques before trying to code it up for the compiler. I will add some more detailed hints on code generation strategies for the various expression types, including multiplication, later in the week.