We have learned in lecture about the representation technique for signed integers in a fixed-width field of binary digits (or bits) called two’s complement. It is not the only such representation, but as compared to the straightforward sign-magnitude style, it has many advantages. In particular, the algorithm for adding two numbers using their two’s complement representations does not require any special treatment of negative numbers (other than the usual checks for overflow): in sign-magnitude form, we would have to branch to handle negatives in a special way.
With this program, you will exercise your understanding of the two’s complement form by implementing conversion between (to and from) standard decimal presentations as well as the addition of two numerals in two’s complement.
The intent is to get you used to working with these forms and values at the lower level of individual bits and bit-fields: these will be crucial skills later in the semester. You should therefore try to implement with your focus at that level. For example, you should use something like an array or array list to store the bits (this mimics the bit field) and something like booleans (or perhaps the integers 0 and 1) to represent the individual bits. (The advantage here to booleans is that we will ultimately be implementing addition using logic gates and circuits, which treat the values that way.)
For this lab you should write a program which does the following:
allow the user to enter two numbers as numerals in base 10, but specifically either positive or negative in sign;
(You should of course check the numerals to ensure they are well-formed, i.e., valid.);
convert the numbers into two’s complement form, in a field of 8 bits (you might allow user-specifiable different numbers of bits as a challenge task);
add the numbers together to get a result of similar form (i.e., a list in
Python or an array or ArrayList in Java, of booleans or small
integers), using the usual right-to-left iterative algorithm with carries
(in other words, the one you learned in grade school, except the only digits
possible are 0 and 1);
convert the result from two’s complement form into decimal for display (including any relevant negative sign)—and please display the actual converted result, even if the calculation overflowed;
use some form of error message or indicator to signal to the user that they have input an invalid numeral, or to the effect that the sum calculation overflowed (in the former case, you don’t need to even attempt the calculation, but as described above, in the overflow case you should proceed and display the erroneous result).
Along the way, it would be nice if you could design an interface that allows for
quick and convenient testing: multiple consecutive trials without restarting the
program, activation of methods using the ‘Enter’ key,
predictable tab order between fields, etc.
In general, try to use the interface yourself, and imagine (and implement!)
whatever would be convenient during a “demo”.
(You’re not required to use a graphical user interface, but I some people may wish to.)
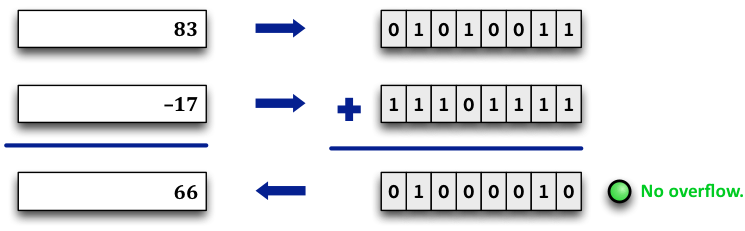
For an idea of what a typical GUI for this lab might look like, look at these diagrams: first, a successful conversion and addition (with correct bits!):

You don’t have to include something that indicates correct function, but you should definitely include an indicator for errors. (And remember to clear the error indicator on the next input!) These errors might come in two forms, either an overflow error in the actual addition:
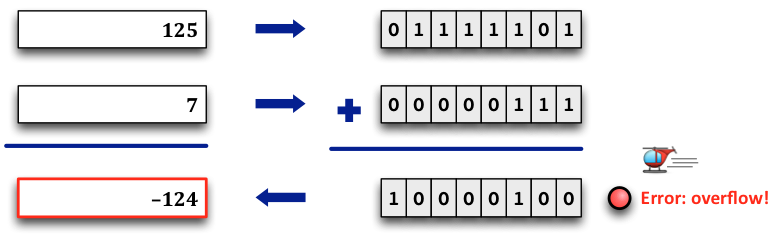
… or a numeral format error in the input, which then can’t be converted or added:
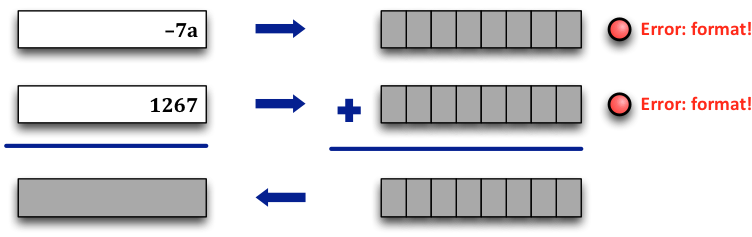
For input/format errors, you need not compute the addition, but for overflow errors, you should show the converted, but erroneous, result (and also indicate that the error occurred).
(And if you need colored “lights” of various kinds to act as indicators, there are some graphics available here.)
For general background on how to implement all of the above steps, check out the various resources on the course home page, including: the explanation of Horner’s technique, the two’s complement clock, the detailed diagram explaining two’s complement conversion, and the diagram explaining reverse Horner conversion.
Note that you should already have code to implement general base conversions, preferably using Horner’s technique, from Lab 1. (Can you use the methods you developed in Lab 1 directly? Did you use Java methods in Lab 1 in the first place? What changes (if any) did you need? How can you make your work more flexible and reusable for the future?)
Assuming the ability to convert numerals, along with some I/O, the process comes down to iterating through a sequence of bits, combining them to produce a result bit (in a parallel sequence), along with some notion of carries. Note that we never need a carry of more than a 1 value (we are just adding two numbers, via their binary numerals), and note that we iterate through the sequence in a right-to-left order. (Finally, note that you might want to implement sequences of 16 or 32 bits as a challenge task, just to show your ability to write more flexible code.)
OK, now for some more specific details: let’s first assume that you are implementing
the data storage for the 8-bit numerals: how should you do this? Clearly something
like an array or a Java ArrayList makes sense: I would recommend arrays,
since we have no need for dynamic length extensions here. But what type should the elements
be? The two obvious candidates are numbers, specifically integers (which would include 0
and 1), or booleans (which would be more direct, if less familiar).
In some sense integers are too much: we should never have to store more than a single bit in an array element, and in fact we should probably never be able to store more than that. Of course it might be convenient to store a 2 or a 3, if only temporarily, as we might come up with such numbers when summing bits and carries during the addition process. But this could also lead to absurd results if you’re not careful, something like a larger integer creeping in for the longer term, and perhaps even appearing in the final result.
(There is also potentially a storage issue here, since we would store a whole Java
integer for just one bit: we could limit this somewhat by using Java’s short
integers (of type short), which are only 16 bits wide, or bytes,
which are only 8 bits … but either way is going to be a bit of bother for
very little savings. Just, please, don’t use
an array of strings to store a mere 8 bits!)
But the best reason to use booleans in this situation is that they better match the point and purpose of the lab: using booleans will encourage you to think in terms of the boolean representations, and especially the boolean operators, that we will have available when we implement similar algorithms at the machine level. (By the way, there’s no guarantee that even booleans will be implemented with single bits in Java, but the storage costs should still be tolerable for this modest application.)
How can you use boolean operations to add numbers? Well, in some sense that’s
the point of the exercise, although if you use arithmetic you are not too far off
the goal. Consider this: you iterate from right to left, and for each of the 8
bit positions, you need to (first approximation) add the bits of the top (t)
and bottom (b) numerals to get two results, the result bit
in the corresponding position (r) and the carry (c) for the next position left:
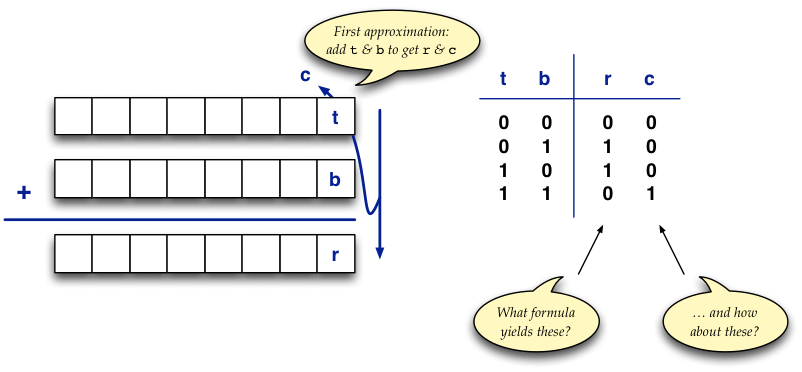
Here I have included a diagram with a truth table to show what boolean function of
two bits is to be computed for each of the result and carry: look at this truth
table and see if you can figure out a short boolean expression that will compute
the appropriate bit value. (Note that in the program, these booleans will
be projected out from the array, and injected back in as well, and will thus look
something more like t[i], b[i], etc. than just bare
variables t and b. Note also that you might use just
a single carry, re-using it for each position … not that it matters that much.)
Ahh, but that’s just the first approximation: of course, after the first bit, you’ll also need to take the carry from the last position into account as part of the inputs. That is to say, the result bit and next carry need to be computed from the top bit, the bottom bit, and the carry from the previous position. This means that you should actually work in terms of a truth table with three input variables and two result columns:
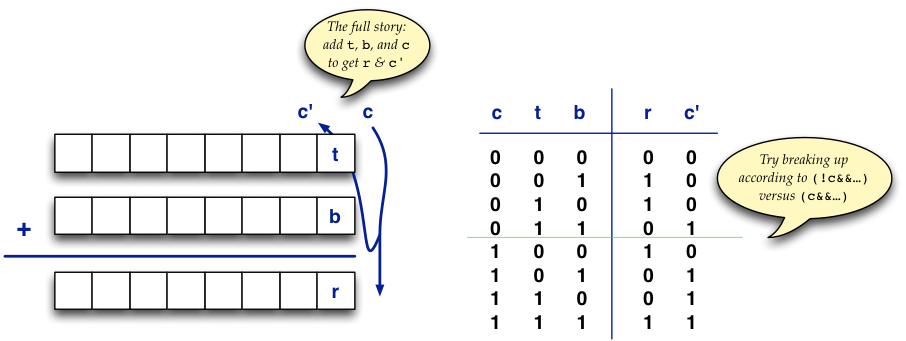
(Perhaps the easiest way to see through to appropriate formulas here is to break the
results up into parts which correspond to cases when the carry bit c is
true versus when it is false: these cases can then be handled in terms of formulæ
of the forms (c && …) and (!c && …).
(Do you see why?)
Finally, remember that adding positive and negative numbers, using two’s complement numerals, simply follows the usual addition algorithm across the bits from right to left, with no need to do anything special to accommodate negatives … well, except for the overflow error condition. And what exactly again is that? It is not just checking whether a carry bit “fell off the end” of the calculation: rather, it is that the sign (bits) of the two arguments are the same, but that of the result bit is different. (Just note that if you do run into an overflow, you should indicate it somehow to the user, but please put the calculated, converted answer into the output field “as is”, to see that it was calculated “correctly”, but also as a debugging aid.)