Developing Natural Numbers   [3]

Adding conversions to and from integers

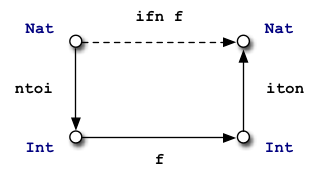
Given the long-winded nature of Nat representations in Haskell, it can be convenient to convert from naturals to integers and back again. We can define conversion functions using Haskell's built-in Int type as follows. Once we have the conversion functions, we can define "round trip" function transformers which convert a function on integers to a function on naturals or vice versa (note that we need separate transformers for unary and binary functions). This gives us a quick-and-dirty way to define functions like addition on naturals, but it's not too informative.

data Nat = Zero | Succ Nat  deriving (Eq, Ord, Show)

nats = iterate Succ Zero

[zero,one,two,three,four,five] = take 6 nats


ntoi  Zero    = 0 :: Int
ntoi (Succ n) = 1 + ntoi n

iton (0::Int) = Zero
iton (i+1)    = Succ (iton i)

ifn f n = iton (f (ntoi n))
nfi f i = ntoi (f (iton i))

ibn b n m = iton (b (ntoi n) (ntoi m))
nbi b i j = ntoi (b (iton i) (iton j))


> ibn (+) two four
Succ (Succ (Succ (Succ (Succ (Succ Zero)))))

Notes

• in order to keep the types simple (i.e., to avoid Num a => qualifiers), we overtly restrict the conversion functions to the Int type
• the type of (for example) ifn is (Int -> Int) -> Nat -> Nat, which can be read as "transforms a function on integers into one on naturals"
• can you guess the type of the binary operator transformer ibn without peeking?
• you can visualize the relationship between a function and its transformation as a "round trip" which takes the long way around the block: