Goals

• To understand complex numbers.
• To understand how fractals are made.
• To use Povray to generate fractals.

Programs

Try running the FractalProject.jar file that you downloaded last week from the \home\classes drive in the folder \gorr\cs142\JarFiles. It allows you to interactively generate and to zoom-in on several different types of fractals.

Create an image you like and save it. Note, the save button on the "Fractal Controls" window does not work - you need to use the pull-down File menu to save. Make sure the image that you want to save is selected (with mouse). Write down the values that were used, e.g. fractal type, xmin, ymin, size, iterations, and parameters (these vary depending on fractal type). Place the image on your web page, including the values that were used.

Imaginary and Complex Numbers

1. Complex numbers are of the form x + i y, where i= .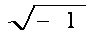
   If z₁ = 2 - 3 i and z₂ = 1 + 7i, Compute the following:

   1. z₁ + z₂
   2. z₁ - z₂
   3. 2*i*z₁
   4. z₁*z₂
   5. | z₁ |    (this is the magnitude of z₁)

2. The Mandelbrot Set: For each point C in the complex plane, one computes the squence of

   z_t = (z_t-1)² + C,    for t = 0, 1, 2, ..., and z₀ = 0. If the magnituded of z_t does not go to infinity as t increases, then we say that C is in the Mandelbrot set.

   For C = 1 + i, what is z₃? What is it's magnitude? It can be shown that if the magnitude ever exceeds 2, then C is not in the Mandelbrot set. Is C in the Mandelbrot set?

Fractals in Povray

1. Review the Povray Fractal examples discussed in class. Experiment by varying each of the parameters: e.g. complex number, type (julia, mandel, ...), exponent, interior parameters, exterior parameters, colors, etc. Try using a fractal in a normal map. Also, try out the 3D fractal object (julia_fractal) and vary its parameters.

2. Create at least 2 images for each of the following:
   1. julia pigment map
   2. mandel pigment map
   3. julia_fractal object
   For each image, save the parameters that were used. Please these 6 images on your web page.

Summary of what to turn in

No later than class time on Thursday, April 19, please do the following:

• Place your fractal image created using FractalProject.jar on your webpage. Include the parameters used to generate the image.
• Be prepared to go over the complex number calculations in class on the board (these will not be collected).
• Place your six fractal images created using povray on your webpage. Include the parameters used to generate the image.
• Email to gorr:
  • your FractalProject.jar image file.
  • one povray fractal image (your favorite).
  Please remember to place "CS-142 Lab 10" in the subject line.

We will look at your images during class on April 19.