Lab 8: Recursion and Divide-and-Conquer Sorting
CS 241: Data Structures, Fall 2007

Goals for this assignment are to:

• Practice induction.
• Understand how to use recursion to implement divide-and-conquer algorithms.
• Understand recursive sorting algorithms.

Reading

Read Chapter 9.

Part 1: Practice Problems

These will not be collected but may appear on an exam. We will go over most of them in class. If you have questions about any of them, please ask!

1. Use induction to prove that:

   

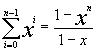
   Recall, to prove this you must 1) state what you are proving, 2) show that the base case is true, 3) state the induction hypothesis, and 4) prove the induction hypothesis is true.

2. Programming Problems:

   1. Write a recursive method to print out a list of numbers (forward and backwards)
   2. Write a recursive method to compute the factorial of n (i.e. n!). How big does n have to be before overflow occurs (note, this depends on the variable type)?
   3. Write a recursive method to calculate the sum given in problem 1 (i.e. not using the formula on the right hand side of the equation). Does your calculation agree with the formula?
   4. Compute the fibonacci series (defined on page 246 in text). How do you use dynamic programming to implement it efficiently?

Part 2: Recursive Sorting

1. Begin with the same sorting animation program you used in lab 7.

2. Mergesort: Add Mergesort to your animation. Note that Mergesort does not sort "in place". As a result, the animation won't work because it relies on the list of numbers being in a single array. However, you can still use the animation program to view the array before and after sorting. Do the following:

   • Read through the description and code in the text starting on page 235.
   • Download MergeSort.java as the starting point for your code. This code differs from the code in the text in the following ways:
     • The code in the text uses arrays while the animation code uses ArrayLists.
     • The run method corresponds to the mergeSort method in the text. You don't need to make any changes to this method.
     • The mergeSort method corresponds to the mergeSortHelper method in the text.
     • The merge method corresponds to the the merge method in the text. You need to implement this method.
   • Be sure to count the number of comparisons. Note that swaps don't really make sense with what is happening so don't bother with them.

3. StoogeSort: Add StoogeSort to the animation program. The algorithm is given by the psuedocode:

   StoogeSort(A,i,j)
   1 if A[i] > A[j]  then exhange A[i] and A[j]
   2 if i+1 >= j then return
   3 k = floor( (j-i+1)/3 )   // Round down
   4 STOOGE-SORT(A,i,j-k)    // First two-thirds
   5 STOOGE-SORT(A,i+k,j)    // Last two-thirds
   6 STOOGE-SORT(A,i,j-k)    // First two-thirds again.
   

   Be sure to count the number of comparisons and swaps. Calculating the number of comparisons is a little tricky. Note, the number of comparison for n=10 should be 364. To speed things up when testing your program, you might want temporarily to set the delay to zero, or just comment out the pause method. Note, the complexity of StoogeSort is Θ(n^2.71).

Part 3: Minesweeper

1. Recall that when you click on a blank cell (i.e. one that has zero mines around it), the program automatically turns over all adjacent empty cells (play the game so you are sure you understand exactly which cells are turned over. This process of turning over cells can be implemented recursively. Think about how this can be done and modify your program to do this. It should not require adding very many lines of code.

Part 4: Extra credit (2 pts)

1. You must first complete parts 1-3 before getting credit for this.

2. As mentioned above, Mergesort does not sort in-place, rather it requires extra memory (what is the space complexity?). However, it can be modified so that it uses much less memory. This modification is described in Problem 9.23 on page 251 of your text. Implement this version of Mergesort in your animation program (call the class MergeSortSpace, or something that easily identifies it - don't over write the original MergeSort). What is the space complexity of this new implementation? Does it change the time complexity?

Evaluation

By Monday, Nov 5, zip together the SortAnimation and Minesweeper projects, including the jar files, and email the code as an attachment to gorr@willamette.edu. Place CS241 Lab 8 in the subject line. Please indicate in your email if you have done the extra credit.

By Thursday, Nov 8 demonstrate the SortAnimation and Minesweeper program to the instructor.