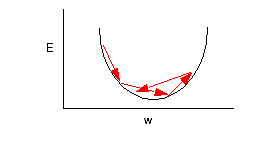
We have seen that online can often be much faster than batch early in the training process. However, the noise in the updates causes the network to bounce around near the minimum and never converge to the very bottom.


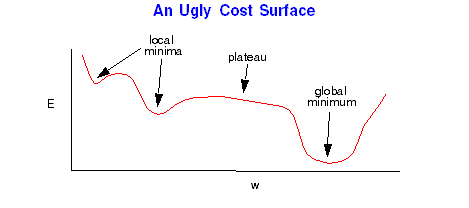
In linear networks the cost function is in the nice shape of a bowl. There is a single minimum. In nonlinear networks, however, the cost surface can be very complex. There can be many minima, valleys, plateau's which make training very difficult. Batch gradient descent will simply move the bottom of the local minimum it randomly starts in. If it is on a plateau, the gradient may be very small and so learning takes a very long time.
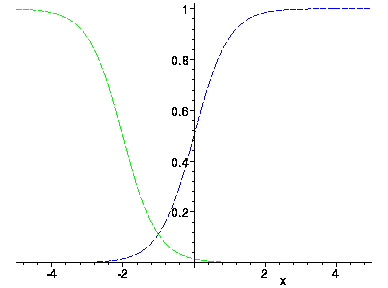
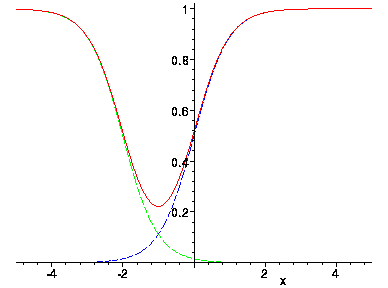
Valleys are common when using sigmoids. Consider what happens when sigmoids are added. Below, the green sigmoid is added to the blue to obtain the red.
The noise in online makes it possible to escape from local minima and plateaus. It can help somewhat with valleys as well.
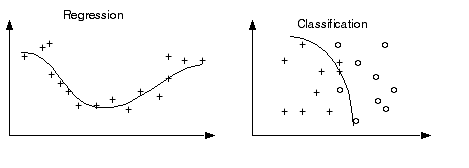
The good news is that multilayer networks can approximate any smooth function as long as you have enough hidden nodes. The bad news is that this added flexibility can cause the network to learn the noise in the data. Consider regression and classification problems where you have a collection of noisy data. The solid line is the "true" function or class boundary and the +'s and o's is the data:
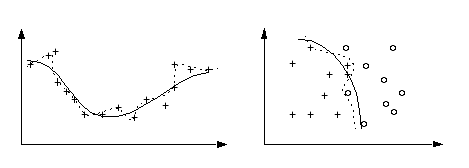
In the above example, the network has not only learned the function but it has also learned the noise present in the data. When the net has learned the noise, we say it has overtrained. The reason for this name is that as a net trains it first learns the rough structure of the data. As it continues to learn, it will pick up the details (i.e. the noise).
Why is overtraining a problem? The whole purpose of training these nets is to be able to predict the function output (regression) or class (classification) for inputs that the net has never seen before (i.e. was not trained on).
A network is said to generalize well if it can accurately predict the correct output on data it has never seen.


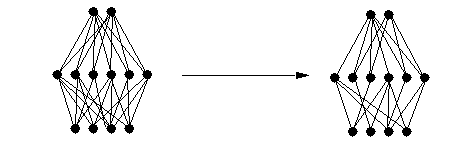
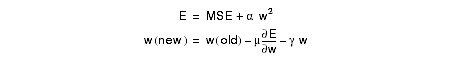
Weight decay pushes the weights toward zero. Note that this corresponds to the linear region of the sigmoid
