![]()
Reinforcement Learning is about learning a mapping from states to a probability distribution over actions. This is called the policy.
Policy = p(s,a) = probability of taking action a when in state s
S = set of all states (assume finite)
st = state at time t
A(st) = set of all possible actions given agent is in state st e S
at = action at time t
rt e R (reals) = reward at time t
At each timestep t=1,2,3,...
The return, rett, is the total reward received starting at time t+1:
rett= rt+1 + rt+2 + rt+3 .... + rf
where rf is the reward at the final time step (can be infinite)
and the discounted return is
rett= rt+1 + g rt+2 + g2 rt+3 ....
where 0 <= g <= 1 is called the discount factor.
We assume that the number of states and actions is finite. We then define the state transition probabilities to be:
![]()
This is just the probability of transitioning from state s to state s' when action a has been taken.
Expected Rewards
![]()
The value function for policy p is

The action-value function for policy p is
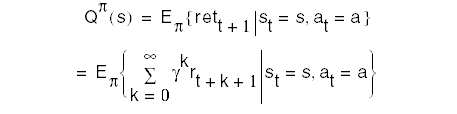
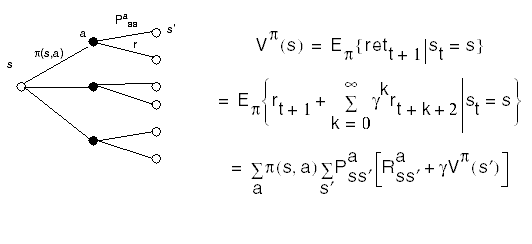
Goal: Find the policy that gives the greatest return over the long run. We say a policy p is better than or equal to policy p' if Vp(s) >= Vp'(s) for all s. There is always at least one such policy. Such a policy it is called an optimal policy and is denoted by p*. Its corresponding value function is called V*:
V*(s) = Vp*(s) = max_p Vp(s) , for all s
and the optimal action-value function
Q*(s,a) = Qp*(s,a) = max_p Qp(s,a) , for all s, a
The Bellman optimality equation is then
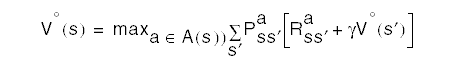
This equation has a unique solution. It is a system of equations with |S| equations and |S| unknowns. If P and R were known then, in principle, it can be solved using some method for solving systems of nonlinear equations. Once V* is known, the optimal policy is determined by always choosing the action that produces the largest V*.
[Top] ![]() [Next: ]
[Next: ] ![]() [Back to the first page]
[Back to the first page]