Math 251W - Foundations of Advanced Math - Syllabus
Class Meetings: MWF 10:20-11:20  in Ford 204

Course Objectives.   Upon successful completion of the course students will be able to:

1. •Describe and identify the logical structure of mathematical proofs and associated constructs, such as logical statements, conditional statements, and quantified statements.
   

2. •Determine the validity of a mathematical argument and identify errors.
   

3. •Apply the appropriate techniques and strategies (such as direct proof of conditional and quantified statements, proof by contrapositive, proof by contraction, proof by exhaustion, uniqueness proofs, and mathematical induction) to prove a proposition.
   

4. •Determine and apply the basic techniques used to disprove false conjectures.
   

5. •Write mathematical arguments in clear, precise, and correct English grammar. Organize arguments effectively.
   

6. •Write, proofread and revise mathematical arguments using LaTeX typesetting.
   

7. •Exhibit fluency with mathematical structures and concepts such as sets, functions, relations, cardinality, and limits of sequences.
   

8. •Paraphrase and explain some famous mathematical ideas, theorems, arguments, proofs, and formulas that every mathematician should know.
   

Textbook. Proofs and Fundamentals; A First Course in Abstract Mathematics, 2nd edition, by Ethan Bloch. There are a few known typos in this text; corrections can be found here.

Course Grades. Your course work will contribute to your course grade according to the following weights.

Homework:                   28% 

Group Exams:               15%

Math Colloquium:            2%

Midterm Exams:            25% 

Final Exam:                   30%

Homework. Homework assignments will be posted on the course WISE site and typically due on Friday unless otherwise stated on the assignment.  Your homework must be written up using LaTeX. An introduction to LaTeX and information about how to download it or use it online can be found here.

Learning to write proofs is difficult!  Please don’t be discouraged by initial failure. Failure is an important part of learning and I expect everyone will get stuck and make mistakes many times throughout the semester.  When this happens, don’t be scared or frustrated, it is a great opportunity for you to learn from your mistakes and try again.  To allow room for mistakes I have devised a rewrite and resubmit process so that your homework grades will reflect what you have learned with lesser emphasis on when you learned it. Here is a description of how this process works.

After your homework is submitted electronically on Friday it will be reviewed by a junior or senior-level math major with exceptional proof writing and reading abilities. This course assistant will read your work and give you feedback in the form of written comments. Typically these comments will be available to you by the following Monday evening. You will then be allowed to polish your work and address any mistakes that you made.  The final draft of this assignment will then be due the following Monday. I recommend working on the current homework assignment Sunday - Friday of each week and using the weekend to polish and fix the assignment that was due the previous week.  Below is a chart that depicts these deadlines and suggested work schedule.  Bring a hardcopy of your polished homework assignment to class to submit on the Monday that it is due.  

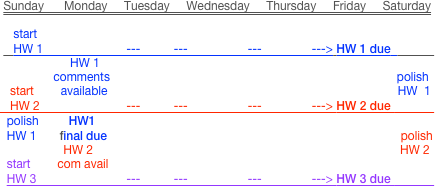
Late Homework policy. If you do not turn in an assignment on the Friday deadline you relinquish the opportunity to receive comments on your assignment from the course assistant and your final submission score may also be decreased by 20%. You may turn in ONE final submission homework assignment late (within one week of when it was due) with no questions and no penalty. All late homework assignments should be clearly labeled with the phrase "Late Math 251 Homework" in the header at the top of the first page. Any late assignment turned in without this phrase might be lost, or confused with garbage and accidentally thrown out.  There is no guaranteed feedback or return date for late homework. Some late assignments may not be graded until the end of the semester.

Group Exams. Group Exams are completed in groups of three, with each group member responsible for solving one of the three exam problems. Each student must proofread their group members’ work and offer suggestions if they believe the solution to be incorrect. At the end of the exam all three group members should know how to do all three problems. Of the 20 points possible for each group exam, 15 will be based on your own solution and 5 will be based on your proofreading. Each student is required to bring a one-sided hand-written page of notes to the group exam to demonstrate that they have spent time preparing to participate in a group activity.

Math Colloquium. You are encouraged to go to many of the Math Department Colloquia this semester, and as part of the course you are required to attend two. Attendance will be taken using a sign-in sheet at each colloquium talk. Cookies and tea will be provided and your courteous attention to the speaker is expected. If your schedule conflicts with all the Colloquia scheduled, please see me for an alternate reading and writing assignment. Most, but not all, Math Colloquia will be Thursday afternoons at 4-5pm.

Midterm Exams, and Final Exam. There will be two midterm exams and a final exam. These exams will be taken individually over the topics and objectives covered thus far in the course. The final will be comprehensive. The dates and times of midterm and final exams are posted on the course schedule.

Study Habits for Success. Consider the following study habits to increase your likelihood of success in this class.

1. 1.Before each class meeting, carefully read each section of the textbook that will be covered. This means you should read to understand big picture ideas, theorem statements, and all definitions, but perhaps not dwell on all the more complicated details of a proof or lengthy example.  Make note of important examples that seem confusing and ask about them in class.  Make note of every definition presented in the text. Math textbooks are extremely dense and reading a math text often requires using new reading strategies. It is often necessary to read a passage several times before the ideas are completely clear. This first read should serve as an introduction to the vocabulary and an overview of some of the bigger concepts or ideas.
   

2. 2.During class you will see some of the material from the textbook for a second time and some new material that is not in the text. Take complete notes especially on the examples not found in the textbook. Please ask questions during class. There are no silly questions. Odds are good that someone else has the same question that you do. (If you are having trouble balancing note taking with critical thinking during class, please ask about the possibility of receiving assistance. If you are an excellent note taker, please consider offering your services to the Learning Center as a way to earn a few bucks for taking excellent class notes.)
   

3. 3.After class, review your notes and carefully reread the section(s) of the textbook covered in class. Work through all details during this reading. This third pass of the material should solidify all important concepts.
   

4. 4.Next, work on the homework problems. Don't expect to be able to sit down and complete all the problems in an hour. Some of the problems will require repeated attempts before you find the solution. I highly recommend starting early and spending several short periods of time on the homework problems that stump you. Coming back to a problem multiple times, even if only for 20 minutes, often leads to deeper understanding, fresh insight and new breakthroughs. Extended study sessions working on problems for hours and hours without breaks can lead to frustration, exhaustion and decreased likelihood for a breakthrough in understanding.
   

5. 5.It is very helpful to form a study group to work on homework problems. Sharing problem solving ideas and approaches is an excellent way to learn.
   

6. 6.If you still feel shaky with the material after following these steps and are unable to complete any of the homework problems, please come see me in office hours as soon as possible.  You are always welcome to stop by during my office hours to ask questions!
   

Course Workload: Willamette's Credit Hour Policy states that for every hour of class time there is an expectation of 2-3 hours work outside of class.  Thus, for a class meeting three hours a week you should anticipate spending 6-9 hours outside of class engaged in course-related activities.  Examples include study time, reading and homework assignments, and group work.  In this class, a typical student may spend as much as 10-12 hours on course work outside of our class meeting times.  If you find that you are studying more than 10 hours and you are unable to complete the assignments, please see me as soon as possible to discuss additional helpful study strategies.

Diversity and Inclusion: Willamette University values diversity and inclusion; we are committed to a climate of mutual respect and full participation. My goal is to create a learning environment that is equitable, inclusive and welcoming. If any aspects of the instruction or design of this course interfere with your inclusion or accurate assessment or achievement, please notify me as soon as possible.

Accessibility and Accommodations: Students with disabilities are encouraged to contact the Accessible Education Services office in Matthews 103 at 503-370-6737 or disb-info@willamette.edu to discuss a range of options to removing barriers in the course, including accommodations. If you are entitled to any kind of accommodation (extra time, non-distracting environment, etc.) during quizzes/exams, please make the appropriate arrangements with me three days before the day of the quiz/exam in question. I will gladly

make necessary accommodations.

Academic Honesty: I am proud to teach at an institution where the students have developed an Honor Code.  It is my expectation that you have read the Honor Code and will abide by this code out of respect for your fellow classmates and for our learning community.

The following definitions are directly from the CLA  Plagiarism and Cheating Policy: Plagiarism is a form of cheating, consists of intentionally or unintentionally representing someone else's work as one's own.  Cheating is any form of intellectual dishonesty or misrepresentation of one's knowledge.

All students must find their own phrasing and wording for the written homework. This is a writing class and all students need to practice writing the solutions to problems using their own words, phrasings and symbols. Plagiarism is not expected and will not be tolerated. Copied homework will earn a grade of zero for all parties involved. I will spend no time attempting to figure out who copied from whom.

Advice from previous Math 251W students to current students: 

1. •“LaTeX does suck for the first assignment, but it gets easier!”
   

2. •“Go to office hours. It helps SO much.”
   

3. •“Take advantage of office hours; they are super productive.”
   

4. •“Make a list of definitions and use them whenever possible when you are trying to prove something.”
   

5. •“GO to office hours.”
   

6. •“Pay attention to the structure of different proofs.”
   

7. •“Start homework way before the due date.”
   

8. •“Start homework early!”
   

9. •“Don’t be afraid to ask for help when you need it, office hours are your friend.”
   

10. • “Look for analogous cases.  They can shorten your proof by around 50%.”
    

11. • “Believe in yourself!”
    

12. • “Attend office hours as much as you possibly can.”
    

13. • “Do NOT wait till the last minute to do LaTeX. It will make you want to die.”
    

14. • “Go to office hours for you health and personal well-being.”
    

15. • “ - Office hours - Go to them.”
    

16. • “Go to office hours.”
    

17. •“If you are stuck on a problem, work on it with a classmate or go to office hours! The problems are hard but often times you can get them when you collaborate with others.”
    

18. •“Put the effort into the homework!!! This is not a class where you can not try on the homework and expect to do well on the tests.”