Euler's method on the TI-82/83
Given a differential equation, say y' = 3x-y, here is how
to make the TI-82/83 draw an Euler's method solution for that differential
equation.
-
We must translate the differential equation: In place of the function (y
in
this case), write Y (upper case), in place of y'
write Y1, and in place of the variable (x in this
case), write X. So we get
Y1=3X-Y.
-
Now press [Y=] and enter our differential equation from
the last step on the first line:
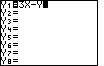
-
Press [WINDOW] to select a suitable window or range. Here's
what I've picked:
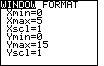
-
Press [PRGM] and select the EULER program.
Press [ENTER]once to paste prgmEULER on
your text screen; press [ENTER] again to run the program.
-
Remember that Euler's method requires an initial condition or starting
point for a solution curve. Suppose, for examples, that the desired
initial condition was y(1) = 4. When the program begins, you must
input that initial condition as follows:
-
When the program asks "X START?", give the x-coordinate
of the initial condition. In our example y(1) = 4, X
START would be 1.
-
When the program asks "Y START?", give the y-coordinate
of the initial condition. In our example y(1) = 4, Y START
would be 4.
-
Euler's method can run forever; you must tell the program when to stop.
If you want a solution curve from X START (1 in the above
example) to, say, 5, you would give "5" for "FINAL X".
-
Finally, give the number of steps desired (so the stepsize works
out to be (FINAL X - X START)/(# of steps) ).
-
Your screen will look something like this before you press [ENTER]
the
last time:
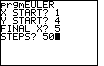
-
When you press [ENTER] the last time, the calculator graphs
an approximate solution curve to the differential equation, for the given
initial condition:
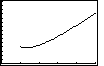
-
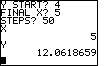
You can get the coordinates of the last point plotted by typing X
[ENTER] [ALPHA] Y [ENTER]:
A more accurate differential equations
solution grapher is available. It is similar to the better methods
built in to the TI-85/86, though not quite as sophisticated. It will generally
require far fewer steps for far greater accuracy.
Last Modified December 8, 1998.
Prof.
Janeba's Home Page | Send comments or questions to: mjaneba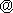 willamette.edu
willamette.edu
Department
of Mathematics | Willamette
University Home Page
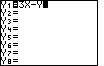

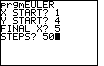


 willamette.edu
willamette.edu