Euler's Method on the TI-86
Given a differential equation, say y' = 3x-y, here is how
to make the TI-86 draw an Euler's method solution curve for that differential
equation.
-
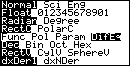
Put the calculator into Differential Equation mode: Press [2nd]
[MODE] and select DifEq as shown:
-
We must translate the differential equation: In place of the function (y
in
this case), write Q1, and in place of the variable (x in
this case), write t. So we get
Q1' = 3t-Q1, or as the calculator wants it, Q'1=3t-Q1.
-
Now press [GRAPH][Q'(t)=] and enter our differential equation
from the last step on the first line:
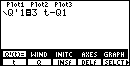
-
Press [EXIT][MORE][FORMT] and make sure that, at the bottom
of the screen, both Euler and FldOff are
selected:

-
Press INITC and enter your initial condition. If
the initial condition was y(1)=4, then since t is
playing the role of x and Q1 is playing the role
of y, we must set tMin=1 and QI1=4:
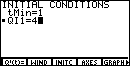
-
Press AXES and tell the calculator which axes to graph.
We will always use x=t and y=Q1 in this
class:
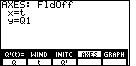
-
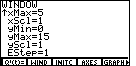
Finally, press [WIND] to select a suitable window:
-
Set
x and y ranges as usual.
-
Set tMin to match what you gave in INITC
above. Usually you will want the range for x and t
to be the same.
-
tStep sets how often points are actually drawn. I'll
pick 0.1 for this example.
-
EStep, at the bottom of the window screen, sets how many
Euler steps are made for each point actually plotted. I'll pick 1.
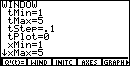
-
Then press
[GRAPH].
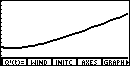
Last Modified December 7, 1998.
Prof.
Janeba's Home Page | Send comments or questions to: mjaneba willamette.edu
willamette.edu
Department
of Mathematics | Willamette
University Home Page



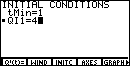

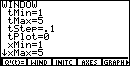

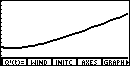
 willamette.edu
willamette.edu