Karel the Robot Learns Python

Ch1   Ch2   Ch3   Ch4   Ch5

Chapter 3
Control Statements

As useful as it is, the ability to define new functions does not actually enable Karel to solve any new problems. The name of a function is merely shorthand for a specific set of instructions. It is therefore always possible to expand a program written as a series of function calls into a single function that accomplishes the same task, although the resulting code is likely to be long and difficult to read. The instructions are still executed in a fixed order that does not depend on the state of Karel’s world.

Before you can solve more interesting problems, you must be able to write programs that transcend this strictly linear, step-by-step operation. To do so, you need to learn several new statements in Karel’s programming language that enable Karel to examine its world and change its execution pattern accordingly.

Statements that affect the order in which a program executes instructions are called control statements. Control statements fall into the following two classes:

1. Conditional statements. Conditional statements specify that certain statements in a program should be executed only if a particular condition holds. In Karel, you specify conditional execution using an if statement.

2. Iterative statements. Iterative statements specify that certain statements in a program should be executed repeatedly, forming what programmers call a loop. Karel supports two iterative statements: a for statement that allows you to repeat a set of instructions a fixed number of times, and a while statement that allows you to repeat a set of instructions as long as some condition holds.

Examining Karel’s world

The conditional and iterative control statements each require that Karel be able to ask questions about its world, such as the following:

• Am I blocked by a wall?
• Are there any beepers on this corner?
• Do I have any beepers in my beeper bag?

Questions such as these are expressed using calls to built-in functions that have yes-or-no answers. In programming, functions that return a yes-or-no answer—which as you will soon discover correspond to the values True and False—are called predicate functions.

Figure 3-1 shows the predicate functions that are built into Karel’s language.

For example, the three questions listed earlier can be expressed in Karel programs like this:

• front_is_blocked()
• beepers_present()
• beepers_in_bag()

Each of the predicate functions requires an empty set of parentheses, just as Karel’s other built-in functions do.

It is also helpful to note that every predicate function in Figure 3-1 is paired with a second one that checks the opposite condition. For example, you can use the front_is_clear function to check whether the path ahead of Karel is clear or the front_is_blocked function to see whether a wall is blocking the way. Choosing the right condition requires you to think about the logic of the problem and figure out which condition is easiest to test.

The if statement

In both Karel and Python, conditional execution is expressed using the if statement, which has one of the two following forms:

or

The first form of the if statement is useful when you want to perform an action only under certain conditions. The second—which comes up less frequently—is appropriate when you need to choose between two alternative courses of action.

The if statement illustrates several features common to all control statements in Karel. The control statement begins with a header that indicates the type of control statement along with any additional information to control the program flow. The lines that are governed by a conditional statement are then indented relative to the header line, conventionally using four spaces. The indented statements represent the body of the control statement.

To give you a sense of where the if statement might come in handy, let’s go back to the pothole-filling program presented at the end of Chapter 2. Before filling the pothole in the fill_pothole function, Karel might want to check whether some other repair crew has already filled the hole on that corner with a beeper. If so, Karel does not need to put down a second one.

You can use the if statement to modify the definition of the fill_pothole function so that Karel puts down a beeper only if there is not already a beeper on that corner. The new definition of fill_pothole looks like this:

It often makes sense to include if statements in a function that check whether it is appropriate to apply that function in the current state of the world. For example, calling the fill_pothole function works correctly only if Karel is facing east directly above a hole. You can use the right_is_clear test to determine whether there is a hole to the south, which is the direction to the right of the one that Karel is facing. The following implementation of fill_pothole includes this test along with the no_beepers_present test you have already seen:

The code in this extended definition of the fill_pothole function shows three different levels of indentation. The body of the entire function is indented four spaces relative to the def keyword that introduces it, everything after the if statement at the top of the function body is executed only if Karel’s right is clear and is therefore indented with four more spaces, and the single line controlled by the no_beepers_present test is indented an additional four spaces.

The indentation makes it easier to see exactly which statements are be affected by a control statement. This indentation is particularly important when the body of a control statement contains other control statements, as in this example. Control statements that occur inside other control statements are said to be nested.

The for statement

The for statement in Karel is used to indicate that you want to repeat a sequence of statements a predetermined number of times. The general form of Karel’s for statement looks like this:

The somewhat convoluted form of the for statement is chosen so that it matches the syntax of the for statement in Python. In Python, you will often have occasion to replace the i in this pattern with a different name. In Karel, it works perfectly well to consider the name i to be part of the required syntax and use it every time you write a for statement.

As a simple illustration of the for statement, you could rewrite the definition of turn_right like this:

Since this definition is not appreciably shorter than the original one that simply repeated turn_left() three times—and the fact that turn_right() is available in the turns library—defining turn_right() in this way is not all that useful. The example does, however, give you a sense of what the for statement does in a context in which its purpose is clear.

To see how the for statement can be used in the context of a programming problem, suppose you wanted to fill every pothole in a road where you were somehow fortunate enough to know the length of the road in advance. Suppose, for example, that the road looked like this:

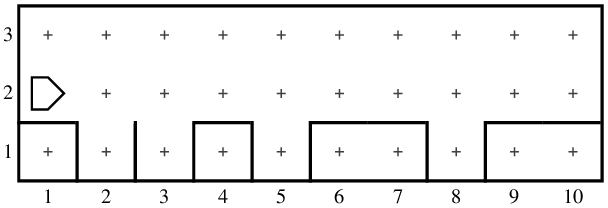
Your mission is to write a program that instructs Karel to fill all ten holes in this road.

Because the statement of the problem tells you that there are exactly ten corners in the world, you can solve this problem by calling the fill_pothole function ten times, once for every corner on 2^nd Street. In between each of those calls, you want Karel to move forward so that it can check and fill any pothole on the next corner.

Although you can certainly use a for statement to accomplish this goal, you can’t write

def fill_ten_potholes(): for i in range(10): fill_pothole() move()

As the icon to the right of the program indicates, this program contains a logical flaw—the sort of error that programmers call a bug. This website and the Python reader use the bug symbol to mark functions that contain errors, to ensure that you don’t accidentally use those examples as models for your own code.

The bug in this particular example illustrates a programming problem called a fencepost error. The name comes from the fact that it takes one more fence post than you might think to fence off a particular distance. How many fence posts, for example, do you need to build a 100-foot fence if the posts are always positioned 10 feet apart? The answer is 11, as illustrated by the following diagram:

The situation facing Karel in the pothole-filling problem has much the same structure. In order to fill potholes in a street that is ten corners long, Karel has to check for ten potholes but only has to move nine times. Because Karel starts and finishes at an end of the roadway, it needs to execute one fewer move instruction than the number of corners it tries to fill. In the fill_ten_potholes program as written, Karel would try to move through the wall at the end of 2^nd Street, which would signal an error.

Once you discover this bug, fixing it is easy. Again, if you know the roadway is ten corners long, you can rewrite the program like this:

The for loop in this revised program executes both the fill_pothole and the move functions for the first nine corners, and then uses a separate fill_pothole call—this one outside the body of the for loop—to check for a pothole under the last corner.

The for statement is useful only when you know in advance the number of repetitions you need to perform. In most applications, the number of repetitions is controlled by the specific nature of the problem. For example, it seems unlikely that a pothole-filling robot could always count on the roadway being exactly ten corners long. It would be much better if Karel could continue to fill holes until it encountered some condition that caused it to stop, such as reaching the end of the street. To write such a program, you need to use the while statement described in the following section.

The while statement

In both Karel and Python, the while statement has the following general form:

As was true for the if, the conditional test is chosen from the set of predicate functions listed in Figure 3-1.

A simple and surprising useful example of the while statement is the function move_to_wall, which looks like this:

When Karel runs the move_to_wall function, it begins by calling front_is_clear to see whether it can move forward. If so, it executes the move function to move forward to the next corner. The program then goes back to the beginning of the while loop and checks the condition again. At some point, the front_is_clear function will indicate that the way forward is not clear, at which point the while loop ends and move_to_wall returns to its caller.

You can use a similar pattern to write a more general solution to the pothole-filling problem, but you have to remember the fencepost problem described in the previous section. Karel has to keep moving as long as the front is clear, but even if it isn’t, it needs to check the last corner for a pothole. The code for fill_all_potholes therefore looks like this:

Figure 3-2 shows an animation of the fill_all_potholes program so that you can trace through its operation.

Ch1   Ch2   Ch3   Ch4   Ch5