


|
Ch1 Ch2 Ch3 Ch4 Ch5 |

|
When you are faced with a complex programming problem, figuring out how to decompose the problem into pieces is usually one of your most important tasks. One of the most productive strategies is called stepwise refinement, which consists of solving problems by starting with the problem as a whole. You break the whole problem down into pieces, and then solve each piece, breaking those down further if necessary.
An exercise in stepwise refinement
Suppose that Karel is initially facing east at the corner of 1st Street and 1st Avenue in a world in which each avenue may contain a vertical tower of beepers of an unknown height, although some avenues may also be empty. Karel’s job is to collect the beepers in each of these towers, and then carry them them all to the easternmost corner of 1st Street. Once there, Karel should put all the beepers into a single pile on that corner and then return to its starting position, as illustrated in the following before-and-after diagram:
| before | after | |
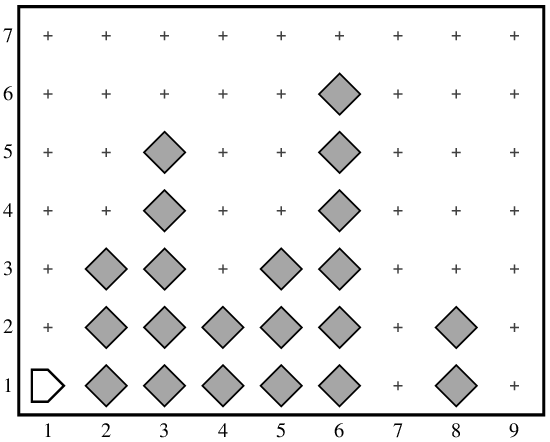 |
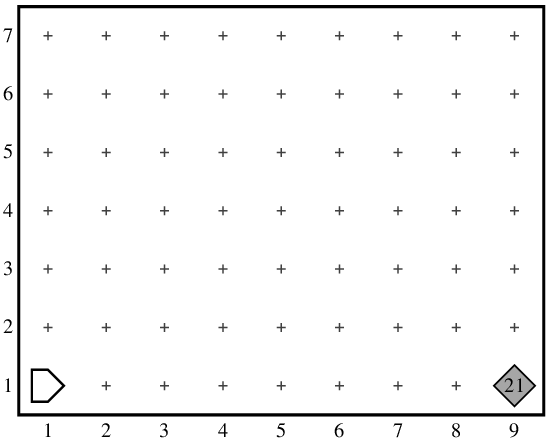 |
The key to solving this problem is to decompose the program in the right way. This task is more complex than the others you have seen, which makes choosing appropriate subproblems more important to obtaining a successful solution.
The principle of top-down design
The central idea in stepwise refinement is that you should start the design of your program from the top, which refers to the level of the program that is conceptually highest and most abstract. At this level, the beeper tower problem is clearly divided into three independent phases. First, Karel has to collect all the beepers. Second, Karel has to deposit them on the last intersection. Third, Karel has to return to its home position. This outline suggests the following decomposition of the problem:
At this level, the problem is easy to understand.
Even though you have not written the code for the functions in the body
of beeper_towers, it is important to
convince yourself that, as long as you believe that the functions you
are about to write will solve the subproblems correctly, you will have a
solution to the problem as a whole.
Refining the first subproblem
Now that you have defined the structure for the program as a
whole, it is time to move on to the first subproblem, which consists of
collecting all the beepers.
This task is itself more complicated than the problems you have seen so
far.
Collecting all the beepers means that you have to pick up the beepers in
every tower until you get to the final corner.
The fact that you need to repeat an operation for each tower suggests
that you need to use a while loop.
But what does this while loop look like?
First of all, you should think about the conditional test.
You want Karel to stop when it hits the wall at the end of the row,
which means that you want Karel to keep going as long as the space in
front is clear.
The collect_all_beepers function will therefore include a
while loop that uses the front_is_clear test.
At each position, you want Karel to collect all the beepers in the tower
beginning on that corner.
If you give that operation a name like collect_one_tower, you can then
write a definition for the collect_all_beepers function even though you haven’t
yet filled in the details.
You do, however, have to be careful.
To avoid the fencepost problem described in Chapter 3, the code must call
collect_one_tower
after the last cycle of the loop, as follows:
As you can see, this function has the same structure as the
fill_all_potholes
function in Figure 3-1.
The only difference is that
collect_all_beepers
calls
collect_one_tower
where the earlier one called fill_pothole.
These two programs are each examples of a general strategy that looks
like this:
You can use this strategy whenever you need to perform an operation on every corner as you move along a path that ends at a wall. If you remember the general strategy, you can quickly write the code whenever you encounter a problem of a similar form. Reusable strategies of this sort come up frequently in programming and are referred to as programming idioms or patterns. The more patterns you know, the easier it will be for you to find one that fits a particular type of problem.
Coding the next level
Even though the code for
collect_all_beepers
is complete, you can’t run the program until you implement
collect_one_tower.
When
collect_one_tower
is called, Karel is standing either at the base of a tower or on an
empty corner.
In the former case, you need to collect the beepers in the tower.
In the latter case, you can simply move on.
The
collect_one_tower
function is still complex enough that an additional level of decomposition
makes sense.
To collect all the beepers in a tower, Karel has to climb the tower to
collect each beeper, turn around, and then return to the wall that
marks the southern boundary of the world.
These steps suggest the following code:
The turn_left instructions
at the beginning and end of the code inside the body of the
if statement are critical to the correctness of this
program.
When
collect_one_tower
is called, Karel is always somewhere on 1st Street facing east.
When it has completed its operation, the program works correctly only if
Karel is once again facing east.
Conditions that must be true prior to a function call are
preconditions; conditions that must apply after the
function finishes are postconditions.
Finishing up
Although the hard work has been done, a few loose ends still need to be resolved because several functions are as yet unwritten. Fortunately, each of these functions can easily be coded without any further decomposition.
Figure 4-1 shows an animation of the
beeper_towers program.
This animation operates a little differently from the ones in the earlier
chapters to emphasize the idea that it is easier to understand large
programs if you think about just one function at a time.
Each time you step into a new function, the animation produces a new
overlay called a stack frame that contains the code
for the function you’re calling.
The new stack frame slides into the trace window, covering up the
stack frame from the previous function.
When the new function returns, its frame goes away, and the program
continues from where it left off.
|

|
Ch1 Ch2 Ch3 Ch4 Ch5 |

|