

|
Ch1 Ch2 Ch3 Ch4 Ch5 |
Although top-down design is a critical strategy for programming, you can’t apply it mechanically without thinking about problem-solving strategies. Figuring out how to solve a particular problem generally requires considerable creativity. The process of designing a solution strategy is traditionally called algorithmic design.
The word algorithm comes from the name of a ninth-century Persian mathematician, Muhammad ibn Mūsā al-Khwārizmī, who developed the first systematic treatment of algebra. You will have a chance to learn more about algorithms throughout your study of computer science.
Even before you have a chance to study algorithms in more detail, it is useful to consider a simple algorithm in Karel’s domain. Suppose, for example, that you want to teach Karel to escape from any maze that contains no loops. In Karel’s world, a maze might look like this:
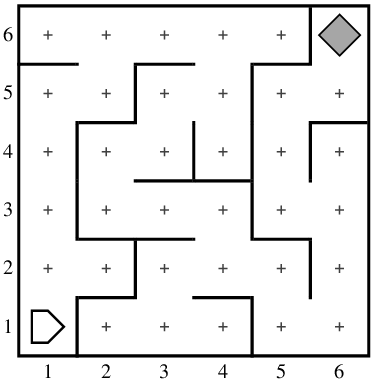
Karel’s job is to navigate the corridors of the maze until it finds the beeper marking the exit. The program, however, must be general enough to solve any loop-free maze, not just the one pictured here.
For any loop-free maze (and in fact for any maze in which no loop surrounds Karel’s initial position), you can use a simple strategy called the right-hand rule, in which you start by putting your right hand on the wall and then go through the maze without ever taking your hand off the wall. Another way to express this strategy is to proceed through the maze one step at a time, always taking the rightmost available path. The program that implements the right-hand rule turns out to be easy to implement in Karel and fits in a single function:
At the beginning of the outer while loop, Karel
turns right to check whether that path is available.
The inner while loop then turns left until an opening
appears.
When that happens, Karel moves forward, and the entire process continues
until Karel reaches the beeper marking the end of the maze.
Figure 5-1 shows an animation of the maze-solving problem.
|

|
Ch1 Ch2 Ch3 Ch4 Ch5 |