Lab 7: Introduction to Complex Numbers
CS 145: Images and Imagination, Spring 2014

Due Date:
Final submission is due Friday, April 11 before class.
This lab is worth 20 points
See policy page for late penalties.

Summary of Goals

The main goals of this lab are to:

Learn about complex numbers .
Learn about Object Oriented Class notation.

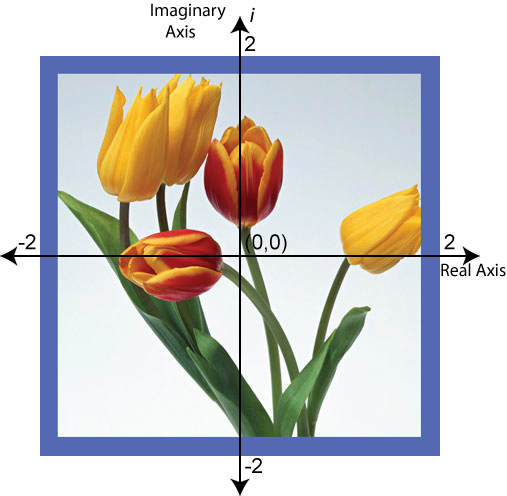
Complex Numbers

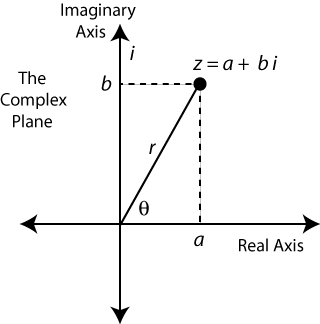	A complex number z can be written in standard form z=a + b i or in polar form as z = r e^{i Θ} = r(cos Θ + i sin Θ )
Figure 1: The Complex Plane

Computing Complex Numbers by Hand: In class, we will go over the origin, definition, and operations of complex numbers. Once you are comfortable with the concepts, work through the following problems: Complex Number Problems (pdf).

These will not be collected but you will be expected to understand how to do them. The answers can be found here (pdf) but it is important that you try to do these without first looking at the solutions! In class, we will go over how these answers were computed. Below, you will also learn how to have Processing calculate the solutions for you.

Complex Numbers Processing Code

In this part of the lab, you will have Processing do the calculations for you. To do this you must:

Include the Complex number class in your program
Learn the syntax for creating and using complex numbers in your code.

Create a new Processing program, and copy Program 1 into it.

Program 1: Complex Number Setup Program

void setup() { Complex z1 = new Complex(5, 8); println("z1 = " + z1); Complex z2 = new Complex(0, 6); println("z2 = " + z2); Complex z = Complex.cMult(z1, Complex.conjugate(z2)); println("z1 * z2_bar = " + z); }

The above program shows how a complex number can be created and used. In class we will go over this notation in more detail. Before you can run this program, you must add the code which defines the complex numbers. We do this next.

Add a new tab to your sketch program and copy in the code below. To add a new tab, press the small arrow next to the name tag (see picture below) and select "New Tab" :

At the bottom where it says "Name for new file:", enter a name (e.g. give it the name "ComplexClass")

Next, paste the code below (Program 2) into this new tab. Note that you need to include this in any program where you use complex numbers. Look through this class and take note of all of the function names. These functions define the available Complex number operations, e.g. conjugate and cMult. You must examine the function declaration to see what parameters it take and what, if anything, it returns.

Program 2: Complex Number Class

// A class representing complex numbers //********************************************************** static class Complex { float real = 0; float imag= 0; Complex() { } Complex(Complex c) { real = c.real; imag = c.imag; } Complex (float r, float i) { real = r; imag = i; } static Complex conjugate(Complex c) { return new Complex(c.real, - c.imag); } static Complex cMult(Complex c1, Complex c2) { float realPart = c1.real*c2.real-c1.imag*c2.imag; float imagPart = c1.real*c2.imag + c2.real*c1.imag; return new Complex(realPart, imagPart); } static Complex fMult(float a, Complex c) { return new Complex(a*c.real, a*c.imag); } static Complex cAdd(Complex c1, Complex c2) { float realPart = c1.real+c2.real; float imagPart = c1.imag+c2.imag; return new Complex(realPart, imagPart); } static Complex cSub(Complex c1, Complex c2) { float realPart = c1.real-c2.real; float imagPart = c1.imag-c2.imag; return new Complex(realPart, imagPart); } // Computes c1/c2 static Complex cDiv(Complex c1, Complex c2) { float topReal = c1.real*c2.real + c1.imag*c2.imag; float topImag = c1.imag*c2.real- c1.real*c2.imag; float bottom = c2.real*c2.real + c2.imag*c2.imag; return new Complex(topReal/bottom, topImag/bottom); } // convert polar coordinates to Cartesian coordinates. static Complex polar2Cart(float r, float degrees) { float realPart = r*cos(radians(degrees)); float imagPart = r*sin(radians(degrees)); return new Complex(realPart, imagPart); } static float len(Complex c) { return sqrt(c.real*c.real+ c.imag*c.imag); } static float angle(Complex c) { if (c.real==0 && c.imag == 0) return 0; else if (c.real >= 0 && c.imag >= 0) return asin( c.imag/len(c)); else if (c.real >= 0 && c.imag <= 0) return 2*PI - asin( -c.imag/len(c)); else if (c.real < 0 && c.imag >= 0) return PI - asin( c.imag/len(c)); else if (c.real < 0 && c.imag < 0) return PI + asin( -c.imag/len(c)); else return 1000; } static Complex cPow(Complex c, float exp) { if (exp==0) return new Complex(1, 0); float r = pow(len(c), exp); float ang = exp*angle(c); Complex cc = polar2Cart(r, ang*180./PI); // println(cc.toString()+" " + c.toString()); return cc; } float zAbs() { return real*real + imag*imag; } String toString() { if (imag ==0) return ""+real; else if (real == 0) return imag + "i" ; else if (imag < 0) return real + " - " + (-imag) + "i"; return real + " + " + imag + "i"; } }

Once you have added this tab, you can run the program. Experiment creating different complex numbers and performing different operations on them. The goal is for you to become comfortable working with the class/object syntax.

Once you understand the syntax, modify the setup program so as to check your answers to written problems 2 through 5.

Complex Transformations

Recall that a complex number can be written in standard form

z = a + b i where a is the value of the real component and b is the value of the imaginary component. A complex number can also be represented in polar form z = r e^{i Θ} where r is its modulus or length, and Θ is the angle it makes .

When you multiply two complex numbers in polar form, you get:

z₁ z₂ = r₁ e^{i Θ₁} r₂ e^{i Θ₂}
= r₁r₂ e^{i (Θ₁+Θ₂)}
= r e^{i Θ} where r = r₁r₂ and angle Θ = (Θ₁+Θ₂)

In other words, multiplying two complex numbers results in a new complex number with modulus r equal to the product of the individual moduli, and angle Θ equal to the sum of the individual angles.

We can also think of multiplication as a transformation. Suppose we are given a complex number z = r e^{i Θ}. We want to transform it by multiplying by another complex number w = s e^{i Φ}. If w has a modulus of s=1, then we get a pure rotation by the angle Φ as shown here:
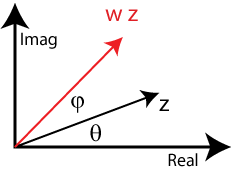z → w z = e^{i Φ} r e^{i Θ} = r e^{i (Φ + Θ)}

Or, instead, if w has an angle Φ=0, then we get a pure scale by s as shown here:
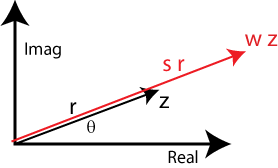z → w z = s e^{i 0} r e^{i Θ} = s r e^{i (Θ)} = s z

In general, multiplying z by w will result in a scale and rotation.

In the image below, we have transformed the image on the left to obtain the image on the right. Each pixel in the image on the left can be thought of as being located in the complex plane at some position z. We can transform the pixel by applying some set of complex operations which take z to z'. We then replace the pixel color at location z with the pixel color at location z'. If z' is outside the bounds of the original image, then we set the pixel color at z to black.

Original Image Transformed Image

To generate similar images of your own, create a new Processing Sketch and copy the code below (Program 3) into your sketch. As was done before, you also need to add a new tab containing the Complex Number class (Program 2). You do not need to understand everything in the code. What you do need to understand is that the code assumes the origin of the complex plane is at the center of the image, and the width of the image is 4, as shown in the image to the right.

The transformation we apply in the code below is z → z' = z^2 + 1. This is set in the function called transform which is highlighted with red text. Your task is to change the contents of this function so that you get the transformations listed below.

Program 3: Complex Image Tranformation

// We assume complex (0,0) is at the center of window // w = width of the displayed complex region float w = 4; // h = height of the displayed complex region float h; // this is set based on aspect ratio of image PImage img; String function; // The is the complex transformation. Currently it is z = z^2 + 1 // TRY CHANGING THIS TO GET A DIFFERENT TRANSFORMED IMAGE Complex transform(Complex c) { return Complex.cAdd(Complex.cPow(c, 2), new Complex(1, 0)); } void setup() { background(0); img = loadImage("flowers.jpg"); // read in image h = w*img.height/img.width; // calc height of complex region img.loadPixels(); // load in pixel colors of the image size(img.width, img.height); // set window size to fit the image. for (int row = 0; row< img.height; row++) { for (int col = 0; col < img.width; col++) { // Determine the complex number associated with this pixel row and col Complex cc = pix2com(col, row); // perform complex transformation cc = transform(cc); // convert the complex cc to its pixel location in the window int[] pt = com2pix(cc); // set the stroke color at (row,col) to be the color // of the image at the transformed value stroke(getColor(pt[0], pt[1])); // draw the point point(col, row); } } save("transformedImage.png"); } // Return the color at pixel (i,j). // If i or j are outside of the image size, then return black color getColor(int i, int j) { if (i < 0 || i > width || j < 0 || j > img.height) return color(0, 0, 0); else return img.get(i, j); } // Convert complex number to a pixel row & col int[] com2pix(Complex c) { int[] p = new int[2]; p[0] = (int) ((c.real+w/2)*img.width/w); p[1] = (int) ((h/2-c.imag)*img.height/h); return p; } // Convert pixel row & col to value in the complex plane Complex pix2com(int i, int j) { j = img.height-j; Complex c = new Complex(); c.real = -w/2 + w * i/img.width; c.imag = -h/2+ h * j/img.height; return c; }

Your Task

Modify the transform function in the code to do the items (1-8) listed below. The images to the right show an example of an original and transformed image. You should use your own image. Use an image which makes the transformation easy to see.

You may use the same Processing sketch for all of the transformations. To do this, it is recommended that you write the transform function so that it contains each of the transformations listed below but only returns the one you specifically want to draw. For example:

Complex transform(Complex c) {
   // Compute translation:
   Complex translation = ....  
	
   // Compute rotation = ...
   Complex rotation = ...
 
   etc ...
 
   // return the name of the one you want to use:
   return translation;   
}

1. Translation: z → z + w, where w=.2 + .4 i
2. Rotation by Θ=45° : z → w*z, where w = e^{i Θ} (Hint: to create w, use the polar2Cart function)
3. Pure scale: z → .5*z,
4. Power: z → z⁵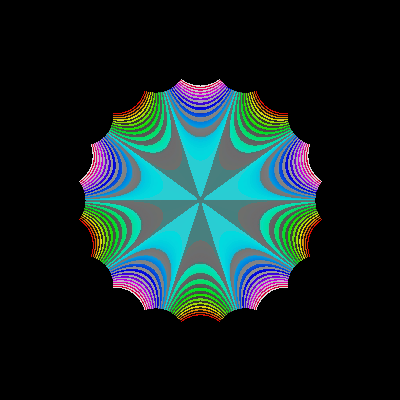
5. Power and translation: z → z³ - 2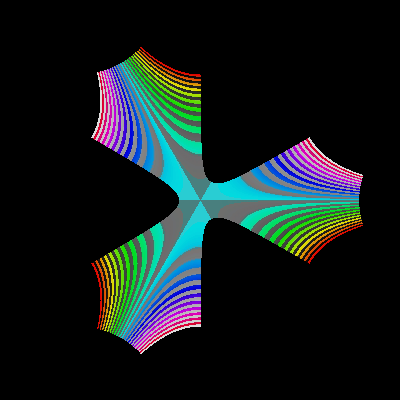
6. Square root: z → √z
7. Inversion: z → 1/z
8. Be Creative! Pick an interesting transformation of your own choosing.

To Be Submitted

At the beginning of class on Friday, April 11:

Place 9 images (the original and the eight transformed) on gorr-classes, in the folder CS145/Lab7/FinalImages. It is important that you name the files by their transformation, e.g. original, scale, translation, etc.
Place the single Processing project containing code for each of the eight transformations on gorr-classes, in the folder CS145/Lab7/ProcessingProjects.
Be prepared to demonstrate your program in class.

Lab 7: Introduction to Complex Numbers CS 145: Images and Imagination, Spring 2014